Fitness Functions¶
Classes for defining fitness functions.
-
class
OneMax[source]¶ Fitness function for One Max optimization problem. Evaluates the fitness of an n-dimensional state vector
![x = [x_{0}, x_{1}, \ldots, x_{n-1}]](../_images/math/089bf4732da9f0cd08d659259afd6ad425f6983b.png) as:
as: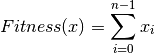
Example
>>> import mlrose >>> import numpy as np >>> fitness = mlrose.OneMax() >>> state = np.array([0, 1, 0, 1, 1, 1, 1]) >>> fitness.evaluate(state) 5
Note
The One Max fitness function is suitable for use in either discrete or continuous-state optimization problems.
-
class
FlipFlop[source]¶ Fitness function for Flip Flop optimization problem. Evaluates the fitness of a state vector
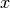 as the total number of pairs of
consecutive elements of
as the total number of pairs of
consecutive elements of 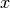 , (
, (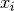 and
and 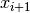 )
where
)
where 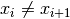 .
.Example
>>> import mlrose >>> import numpy as np >>> fitness = mlrose.FlipFlop() >>> state = np.array([0, 1, 0, 1, 1, 1, 1]) >>> fitness.evaluate(state) 3
Note
The Flip Flop fitness function is suitable for use in discrete-state optimization problems only.
-
class
FourPeaks(t_pct=0.1)[source]¶ Fitness function for Four Peaks optimization problem. Evaluates the fitness of an n-dimensional state vector
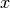 , given parameter T, as:
, given parameter T, as: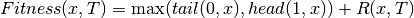
where:
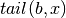 is the number of trailing b’s in
is the number of trailing b’s in 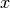 ;
;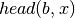 is the number of leading b’s in
is the number of leading b’s in 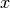 ;
;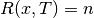 , if
, if 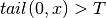 and
and
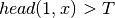 ; and
; and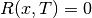 , otherwise.
, otherwise.
Parameters: t_pct (float, default: 0.1) – Threshold parameter (T) for Four Peaks fitness function, expressed as a percentage of the state space dimension, n (i.e. 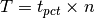 ).
).Example
>>> import mlrose >>> import numpy as np >>> fitness = mlrose.FourPeaks(t_pct=0.15) >>> state = np.array([1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0]) >>> fitness.evaluate(state) 16
References
De Bonet, J., C. Isbell, and P. Viola (1997). MIMIC: Finding Optima by Estimating Probability Densities. In Advances in Neural Information Processing Systems (NIPS) 9, pp. 424–430.
Note
The Four Peaks fitness function is suitable for use in bit-string (discrete-state with
max_val = 2) optimization problems only.
-
class
SixPeaks(t_pct=0.1)[source]¶ Fitness function for Six Peaks optimization problem. Evaluates the fitness of an n-dimensional state vector
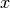 , given parameter T, as:
, given parameter T, as: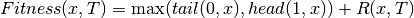
where:
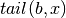 is the number of trailing b’s in
is the number of trailing b’s in 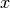 ;
;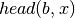 is the number of leading b’s in
is the number of leading b’s in 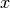 ;
;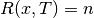 , if (
, if (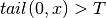 and
and
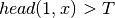 ) or (
) or (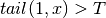 and
and
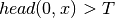 ); and
); and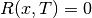 , otherwise.
, otherwise.
Parameters: t_pct (float, default: 0.1) – Threshold parameter (T) for Six Peaks fitness function, expressed as a percentage of the state space dimension, n (i.e. 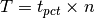 ).
).Example
>>> import mlrose >>> import numpy as np >>> fitness = mlrose.SixPeaks(t_pct=0.15) >>> state = np.array([0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1]) >>> fitness.evaluate(state) 12
References
De Bonet, J., C. Isbell, and P. Viola (1997). MIMIC: Finding Optima by Estimating Probability Densities. In Advances in Neural Information Processing Systems (NIPS) 9, pp. 424–430.
Note
The Six Peaks fitness function is suitable for use in bit-string (discrete-state with
max_val = 2) optimization problems only.
-
class
ContinuousPeaks(t_pct=0.1)[source]¶ Fitness function for Continuous Peaks optimization problem. Evaluates the fitness of an n-dimensional state vector
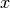 , given parameter T,
as:
, given parameter T,
as: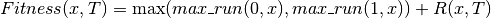
where:
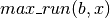 is the length of the maximum run of b’s
in
is the length of the maximum run of b’s
in 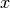 ;
;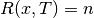 , if (
, if (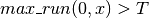 and
and
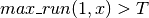 ); and
); and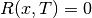 , otherwise.
, otherwise.
Parameters: t_pct (float, default: 0.1) – Threshold parameter (T) for Continuous Peaks fitness function, expressed as a percentage of the state space dimension, n (i.e. 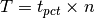 ).
).Example
>>> import mlrose >>> import numpy as np >>> fitness = mlrose.ContinuousPeaks(t_pct=0.15) >>> state = np.array([0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 1]) >>> fitness.evaluate(state) 17
Note
The Continuous Peaks fitness function is suitable for use in bit-string (discrete-state with
max_val = 2) optimization problems only.
-
class
Knapsack(weights, values, max_weight_pct=0.35)[source]¶ Fitness function for Knapsack optimization problem. Given a set of n items, where item i has known weight
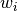 and known value
and known value
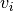 ; and maximum knapsack capacity,
; and maximum knapsack capacity, 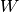 , the Knapsack
fitness function evaluates the fitness of a state vector
, the Knapsack
fitness function evaluates the fitness of a state vector
![x = [x_{0}, x_{1}, \ldots, x_{n-1}]](../_images/math/089bf4732da9f0cd08d659259afd6ad425f6983b.png) as:
as: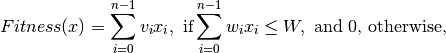
where
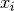 denotes the number of copies of item i included in the
knapsack.
denotes the number of copies of item i included in the
knapsack.Parameters: - weights (list) – List of weights for each of the n items.
- values (list) – List of values for each of the n items.
- max_weight_pct (float, default: 0.35) – Parameter used to set maximum capacity of knapsack (W) as a percentage
of the total of the weights list
(
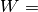 max_weight_pct
max_weight_pct 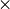 total_weight).
total_weight).
Example
>>> import mlrose >>> import numpy as np >>> weights = [10, 5, 2, 8, 15] >>> values = [1, 2, 3, 4, 5] >>> max_weight_pct = 0.6 >>> fitness = mlrose.Knapsack(weights, values, max_weight_pct) >>> state = np.array([1, 0, 2, 1, 0]) >>> fitness.evaluate(state) 11
Note
The Knapsack fitness function is suitable for use in discrete-state optimization problems only.
-
class
TravellingSales(coords=None, distances=None)[source]¶ Fitness function for Travelling Salesman optimization problem. Evaluates the fitness of a tour of n nodes, represented by state vector
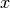 , giving the order in which the nodes are visited, as the total
distance travelled on the tour (including the distance travelled between
the final node in the state vector and the first node in the state vector
during the return leg of the tour). Each node must be visited exactly
once for a tour to be considered valid.
, giving the order in which the nodes are visited, as the total
distance travelled on the tour (including the distance travelled between
the final node in the state vector and the first node in the state vector
during the return leg of the tour). Each node must be visited exactly
once for a tour to be considered valid.Parameters: - coords (list of pairs, default: None) – Ordered list of the (x, y) coordinates of all nodes (where element i
gives the coordinates of node i). This assumes that travel between
all pairs of nodes is possible. If this is not the case, then use
distancesinstead. - distances (list of triples, default: None) – List giving the distances, d, between all pairs of nodes, u and v, for
which travel is possible, with each list item in the form (u, v, d).
Order of the nodes does not matter, so (u, v, d) and (v, u, d) are
considered to be the same. If a pair is missing from the list, it is
assumed that travel between the two nodes is not possible. This
argument is ignored if coords is not
None.
Examples
>>> import mlrose >>> import numpy as np >>> coords = [(0, 0), (3, 0), (3, 2), (2, 4), (1, 3)] >>> dists = [(0, 1, 3), (0, 2, 5), (0, 3, 1), (0, 4, 7), (1, 3, 6), (4, 1, 9), (2, 3, 8), (2, 4, 2), (3, 2, 8), (3, 4, 4)] >>> fitness_coords = mlrose.TravellingSales(coords=coords) >>> state = np.array([0, 1, 4, 3, 2]) >>> fitness_coords.evaluate(state) 13.86138... >>> fitness_dists = mlrose.TravellingSales(distances=dists) >>> fitness_dists.evaluate(state) 29
Note
- The TravellingSales fitness function is suitable for use in travelling salesperson (tsp) optimization problems only.
- It is necessary to specify at least one of
coordsanddistancesin initializing a TravellingSales fitness function object.
-
evaluate(state)[source]¶ Evaluate the fitness of a state vector.
Parameters: state (array) – State array for evaluation. Each integer between 0 and (len(state) - 1), inclusive must appear exactly once in the array. Returns: fitness (float) – Value of fitness function. Returns np.infif travel between two consecutive nodes on the tour is not possible.
- coords (list of pairs, default: None) – Ordered list of the (x, y) coordinates of all nodes (where element i
gives the coordinates of node i). This assumes that travel between
all pairs of nodes is possible. If this is not the case, then use
-
class
Queens[source]¶ Fitness function for N-Queens optimization problem. Evaluates the fitness of an n-dimensional state vector
![x = [x_{0}, x_{1}, \ldots, x_{n-1}]](../_images/math/089bf4732da9f0cd08d659259afd6ad425f6983b.png) , where
, where 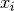 represents the row position (between 0 and n-1, inclusive) of the ‘queen’
in column i, as the number of pairs of attacking queens.
represents the row position (between 0 and n-1, inclusive) of the ‘queen’
in column i, as the number of pairs of attacking queens.Example
>>> import mlrose >>> import numpy as np >>> fitness = mlrose.Queens() >>> state = np.array([1, 4, 1, 3, 5, 5, 2, 7]) >>> fitness.evaluate(state) 6
References
Russell, S. and P. Norvig (2010). Artificial Intelligence: A Modern Approach, 3rd edition. Prentice Hall, New Jersey, USA.
Note
The Queens fitness function is suitable for use in discrete-state optimization problems only.
-
class
MaxKColor(edges)[source]¶ Fitness function for Max-k color optimization problem. Evaluates the fitness of an n-dimensional state vector
![x = [x_{0}, x_{1}, \ldots, x_{n-1}]](../_images/math/089bf4732da9f0cd08d659259afd6ad425f6983b.png) , where
, where 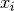 represents the color of node i, as the number of pairs of adjacent nodes
of the same color.
represents the color of node i, as the number of pairs of adjacent nodes
of the same color.Parameters: edges (list of pairs) – List of all pairs of connected nodes. Order does not matter, so (a, b) and (b, a) are considered to be the same. Example
>>> import mlrose >>> import numpy as np >>> edges = [(0, 1), (0, 2), (0, 4), (1, 3), (2, 0), (2, 3), (3, 4)] >>> fitness = mlrose.MaxKColor(edges) >>> state = np.array([0, 1, 0, 1, 1]) >>> fitness.evaluate(state) 3
Note
The MaxKColor fitness function is suitable for use in discrete-state optimization problems only.
-
class
CustomFitness(fitness_fn, problem_type='either', **kwargs)[source]¶ Class for generating your own fitness function.
Parameters: - fitness_fn (callable) – Function for calculating fitness of a state with the signature
fitness_fn(state, **kwargs). - problem_type (string, default: ‘either’) – Specifies problem type as ‘discrete’, ‘continuous’, ‘tsp’ or ‘either’ (denoting either discrete or continuous).
- kwargs (additional arguments) – Additional parameters to be passed to the fitness function.
Example
>>> import mlrose >>> import numpy as np >>> def cust_fn(state, c): return c*np.sum(state) >>> kwargs = {'c': 10} >>> fitness = mlrose.CustomFitness(cust_fn, **kwargs) >>> state = np.array([1, 2, 3, 4, 5]) >>> fitness.evaluate(state) 150
- fitness_fn (callable) – Function for calculating fitness of a state with the signature